Travelling to work
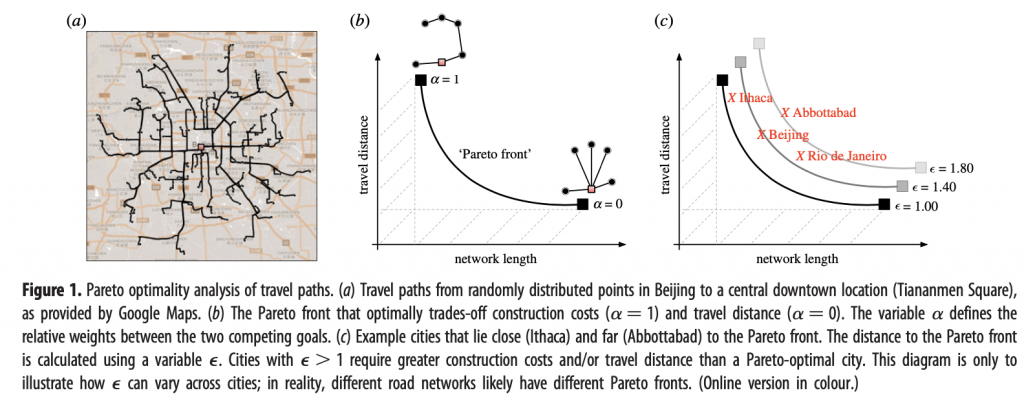
The easiest trade-offs to consider are those where there is a simple and obvious mathematical model to compare with reality. A good example is “travel to work” (Suen and Navlakha 2019).
People live in various parts of a city and travel in to the centre every day.
The expensive solution is many roads to the centre, one for each person. The total length of road is large although each journey is short.
The cheap solution is a single road linking all the people with the middle of the city. The road is shorter but most journeys are longer, especially for the person living at the far end of the road.
The trade-off is a branching road network linking all the people with the city centre, minimising both the total length of road and the average of the distance travelled by each user.
For a given distribution of people, the length of road for the two extremes plus a number of intermediate networks can be calculated and the distances plotted. The resulting curve – the Pareto Front – represents the best design of the road network for all possibilities given the distribution of people.
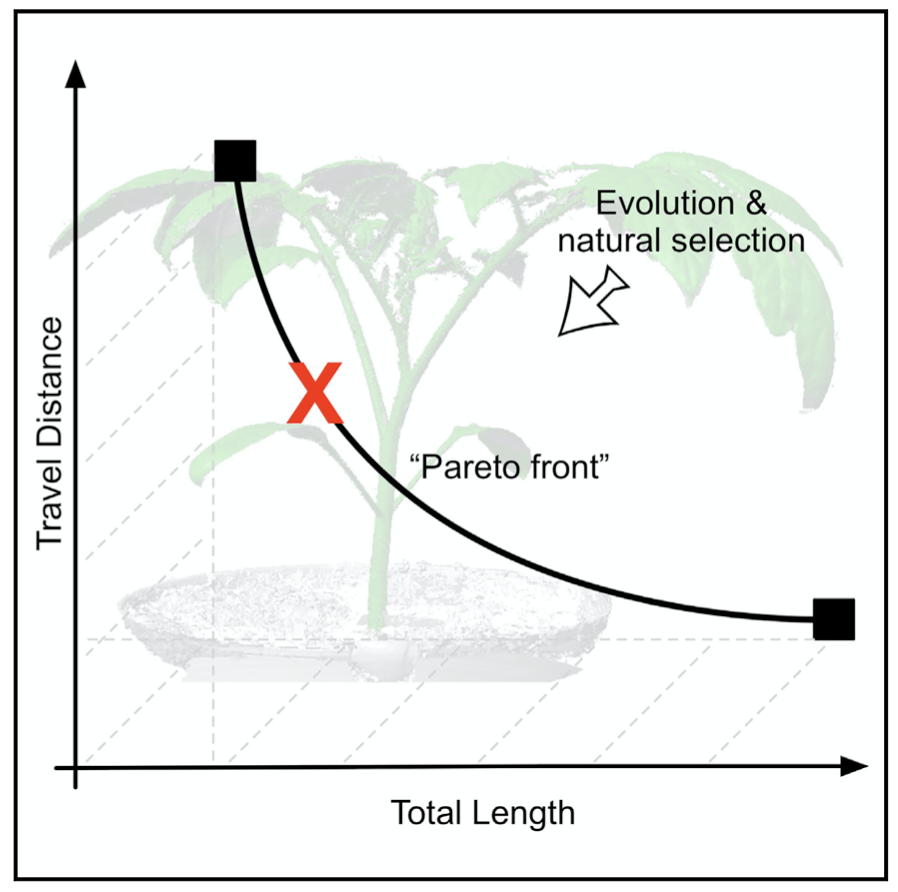
A closely similar case is the venation of a leaf, where points around the leaf are connected to the stem. Modelling and analysis again produce a Pareto Front (Conn et al. 2017 https://pubmed.ncbi.nlm.nih.gov/28750198/).
The trade-off is a universal statement of a problem. In order for this to be useful, it is necessary to know what factors can be used to design or maintain a trade-off.
